INTRODUCCIÓN A LA
ESTADÍSTICA DESCRIPTIVA.
Objetivo: Conocer las técnicas de recolección, tabulación, clasificación y codificación de la información cualitativa (atributo) y cuantitativa (variable), a través de la observación y procesamiento de los datos estadísticos.
HISTORIA DE LA ESTADÍSTICA
RAMAS DE LA ESTADÍSTICA.
TIPOS DE VARIABLES.
Cualitativas o Atributos: No se pueden medir numéricamente (por ejemplo: nacionalidad , color de piel, sexo , etc.).
Cuantitativas: Tienen valor numérico (edad, precio de un producto, ingresos anuales). Las variables cuantitativas se pueden clasificar en:
* Discretas: solo pueden sumar valores enteros.
* Continuas: Pueden tomar cualquier valor real dentro de un intervalo.
CONCEPTOS USADOS PARA EL ESTUDIO DE LAS VARIABLES.
INDIVIDUO, POBLACIÓN Y MUESTRA.
- Individuo: Cualquier elemento que porte información sobre el fenómeno que se estudia. Así, si se estudia la altura de los niños de una clase, cada alumno es un individuo; si se estudia el precio de autos, cada auto es un individuo.
- Población: Conjunto de todos los individuos (personas, objetos, animales, etc.) que porten información sobre el fenómeno que se estudia. Ej. si se estudia el precio de la vivienda en una ciudad, la población sera el total de viviendas de dicha ciudad.
- Muestra: Subconjunto que se selecciona de la población. Ej. si se estudia el precio de la vivienda de una ciudad, se selecciona un subgrupo lo suficientemente representativo para portar la información sobre el fenómeno que se estudia.
FUENTES DE INFORMACIÓN
LA ESTADÍSTICA EN COLOMBIA.
La recolección, procesamiento y análisis estadístico en nuestro país la ejecuta el Departamento Administrativo Nacional Estadística DANE.
Las Funciones de DANE, están establecidas por la ley 489 de 1998 y el decreto 262 del 28 de enero de 2004, este último contempla cuatro ramas generales en las que se enmarcan dichas funciones.
FUNCIONES DEL DANE
1. Número de personas que hizo la degustación.
2. Variable cualitativa en estudio.
SABOR (X)
3. Tabla de distribución de frecuencias "Chocolates Universal"
Otra técnica usada para la representación de datos estadísticos, es la tabla de distribución de frecuencias para datos agrupados.
Número de intervalos
m = 1+3.3 log(50)
m ≈ 6
Rango:
r = 164-103= 61
Valor Máximo: 164
Valor Mínimo: 103
Longitud del intervalo
A= 61/6
A≈ 10
Interpretación de datos
f1 = 5 significa que hay 5 estudiantes que pesan entre 102-112 libras
h3 = 0.18 significa que el 18% de los estudiantes pesan entre 124 y 134 libras
F3 = 22 significa que hay 22 estudiantes que pesan 134 libras o menos
H2 = 0,26 significa que el 26% de estudiantes registrados pesan 123 libras o menos
Mc3 = 129 significa que 9 estudiantes pesan en promedio 129 libras
Resumen de la información
La información contenida en una matriz de datos la podemos resumir por valores estadísticos los cuales se obtienen a través de funciones de datos y se clasifican en: estadísticos de localización, estadísticos de escala, estadísticos de forma y estadísticos de asociación.
Valores estadísticos de localización:
Nos indican en donde se localizan los datos de una variable dentro del rango de valores.
Entre ellos encontramos la media aritmética, la mediana y la moda.
Media aritmética: se entiende por media aritmética de una distribución de datos a la relacion entre la suma de los valores de la distribución (x) y el número de los mismos (n)
Comúnmente se la representa con una X barrada .
Para hallar la media aritmética se utilizan las siguientes fórmulas dependiendo de donde se tomen los datos a analizar:
Tomando los datos directamente de la matriz.
Tomando los datos de la tabla de distribución de frecuencias.
Tomandolos desde los datos agrupados en intervalos de clase.
Ejemplo de Media Aritmética por intervalos de clase.
La Mediana (Me): La mediana de una serie de datos ordenados es el valor central de la distribución de datos, es decir aquel valor que tiene tantas observaciones anteriores como posteriores a él.
Cuando el número de valores es impar la mediana esta bien definida, pues existe un valor central y se determina con la siguiente fórmula.
Si por el contrario el número de valores es par, se toma como mediana el valor medio de los dos valores centrales de igual forma que el caso anterior la mediana la podemos hallar aplicando la siguiente fórmula.
Otra forma de hallar la mediana por medio de datos agrupados en intervalos de clase es la siguiente.
Continuando con el análisis de los datos del peso de los estudiantes y aplicando la fórmula anterior podemos determinar que la mediana es 137,3 libras.
La información obtenida para un estudio o investigación debe ser sometida a un análisis cuidadoso que permita hacer comentarios interpretativos. según su procedencia, la información estadística se clasifica en:
- Información de fuentes primarias: Cuando el planteamiento del problema e hipótesis acompaña el diseño de las técnicas para obtener datos que permiten probar la hipótesis (encuestas, entrevistas), se tiene conocimiento de la metodología utilizada para recolectar datos, esto ayuda a la interpretación de los mismos.
- Información de fuentes secundarias: Cuando el planteamiento y la hipótesis se plantean en un momentos posterior a la existencia de los datos (historias clínicas, archivos del DANE, material de consulta).
TÉCNICAS DE RECOLECCIÓN DE INFORMACIÓN
LA ESTADÍSTICA EN COLOMBIA.
La recolección, procesamiento y análisis estadístico en nuestro país la ejecuta el Departamento Administrativo Nacional Estadística DANE.
Las Funciones de DANE, están establecidas por la ley 489 de 1998 y el decreto 262 del 28 de enero de 2004, este último contempla cuatro ramas generales en las que se enmarcan dichas funciones.
FUNCIONES DEL DANE
- Producción de estadísticas estratégicas.
- Síntesis de Cuentas Nacionales.
- Producción y difusión de información oficial básica.
- Difusión y Cultura Estadística.
Ejemplo de la distribución de los
valores de una variable
Una fábrica de chocolates
va a sacar una chocolatina con un relleno nuevo. Para ello, decide hacer
degustaciones de cuatro chocolatinas con rellenos diferentes en un supermercado
y pide a las personas que escojan entre la chocolatina A, B, C o D.
- La chocolatina A tiene relleno de fresa.
- La chocolatina B tiene relleno de arequipe.
- La chocolatina C tiene relleno de amareto.
- La chocolatina D tiene relleno de maracuyá.
Los siguientes fueron los resultados de la degustación.
1. Número de personas que hizo la degustación.
n = 60
2. Variable cualitativa en estudio.
3. Tabla de distribución de frecuencias "Chocolates Universal"
4. Diagrama de barras de datos.
Otra técnica usada para la representación de datos estadísticos, es la tabla de distribución de frecuencias para datos agrupados.
El
departamento médico de una universidad realiza el registro del peso de los
estudiantes que hacen parte de los equipos que competirán en los juegos
interuniversitarios.
Número de intervalos
m = 1+3.3 log(50)
m ≈ 6
Rango:
r = 164-103= 61
Valor Máximo: 164
Valor Mínimo: 103
Longitud del intervalo
A= 61/6
A≈ 10
f1 = 5 significa que hay 5 estudiantes que pesan entre 102-112 libras
h3 = 0.18 significa que el 18% de los estudiantes pesan entre 124 y 134 libras
F3 = 22 significa que hay 22 estudiantes que pesan 134 libras o menos
H2 = 0,26 significa que el 26% de estudiantes registrados pesan 123 libras o menos
Mc3 = 129 significa que 9 estudiantes pesan en promedio 129 libras
Resumen de la información
MEDIDAS DE TENDENCIA CENTRAL
La información contenida en una matriz de datos la podemos resumir por valores estadísticos los cuales se obtienen a través de funciones de datos y se clasifican en: estadísticos de localización, estadísticos de escala, estadísticos de forma y estadísticos de asociación.
Nos indican en donde se localizan los datos de una variable dentro del rango de valores.
Entre ellos encontramos la media aritmética, la mediana y la moda.
Media aritmética: se entiende por media aritmética de una distribución de datos a la relacion entre la suma de los valores de la distribución (x) y el número de los mismos (n)
Comúnmente se la representa con una X barrada .
Para hallar la media aritmética se utilizan las siguientes fórmulas dependiendo de donde se tomen los datos a analizar:
Tomando los datos directamente de la matriz.
Tomando los datos de la tabla de distribución de frecuencias.
Tomandolos desde los datos agrupados en intervalos de clase.
Ejemplo de Media Aritmética por intervalos de clase.
Cuando el número de valores es impar la mediana esta bien definida, pues existe un valor central y se determina con la siguiente fórmula.
Si por el contrario el número de valores es par, se toma como mediana el valor medio de los dos valores centrales de igual forma que el caso anterior la mediana la podemos hallar aplicando la siguiente fórmula.
Otra forma de hallar la mediana por medio de datos agrupados en intervalos de clase es la siguiente.
Continuando con el análisis de los datos del peso de los estudiantes y aplicando la fórmula anterior podemos determinar que la mediana es 137,3 libras.
n = 50
Ej = 135
Fj-1 = 22
fj = 13
A = 10
Moda (Mo) La moda nos permite identificar el valor que se presenta con más frecuencia en la muestra, o en pocas palabras el que más se repite. En algunos casos puede no existir. en otros puede ser única (Unimodal) o no (bimodal).
Cuando los datos están agrupados en intervalos de clase: primero se localiza el intervalo con mayor frecuencia absoluta el cual es llamado Intervalo Modal (lj) y la moda se obtiene a través de:
MEDIDAS DE LOCALIZACIÒN
Cuartiles, Deciles, Percentiles
- Cuartil
Q1. Cuartil 1.
Q3. Cuartil 3.
- Deciles
D5. Decil 5.
Percentiles
P25. Percentil 25.
Estadísticos de escala.
Rango: Este término corresponde a la diferencia entre el dato mayor y el dato menor del conjunto.
Rango = Xmax - Xmin.
Rango = 164 - 103 = 61
Valor Máximo: 164
Valor Mínimo: 103
Rango Intercuartílico: Para evitar la influencia de los valores externos (max y min) atípicos se pueden analizar solamente los valores intermedios del conjunto de datos.
El Rango Intercuartílico toma solamente el 50 % de los datos centrales de la distribución, correspondientes al Q3 y Q1 o P75 y P25.
Q3=148,77
Q1= 122,37
RIQ= 148,77 - 122,37
RIQ= 26,4
MEDIDAS DE DISPERSIÓN
Estadísticos de escala que dependen de la media.
Desviación media: DM
Varianza: Promedio de los cuadrados de las desviaciones medias alrededor de la media
Desviación Estándar: Indica que tan variables es un conjunto de datos. Cuanto mayor sea la desviación, mas dispersos están los datos.
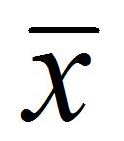
No hay comentarios.:
Publicar un comentario